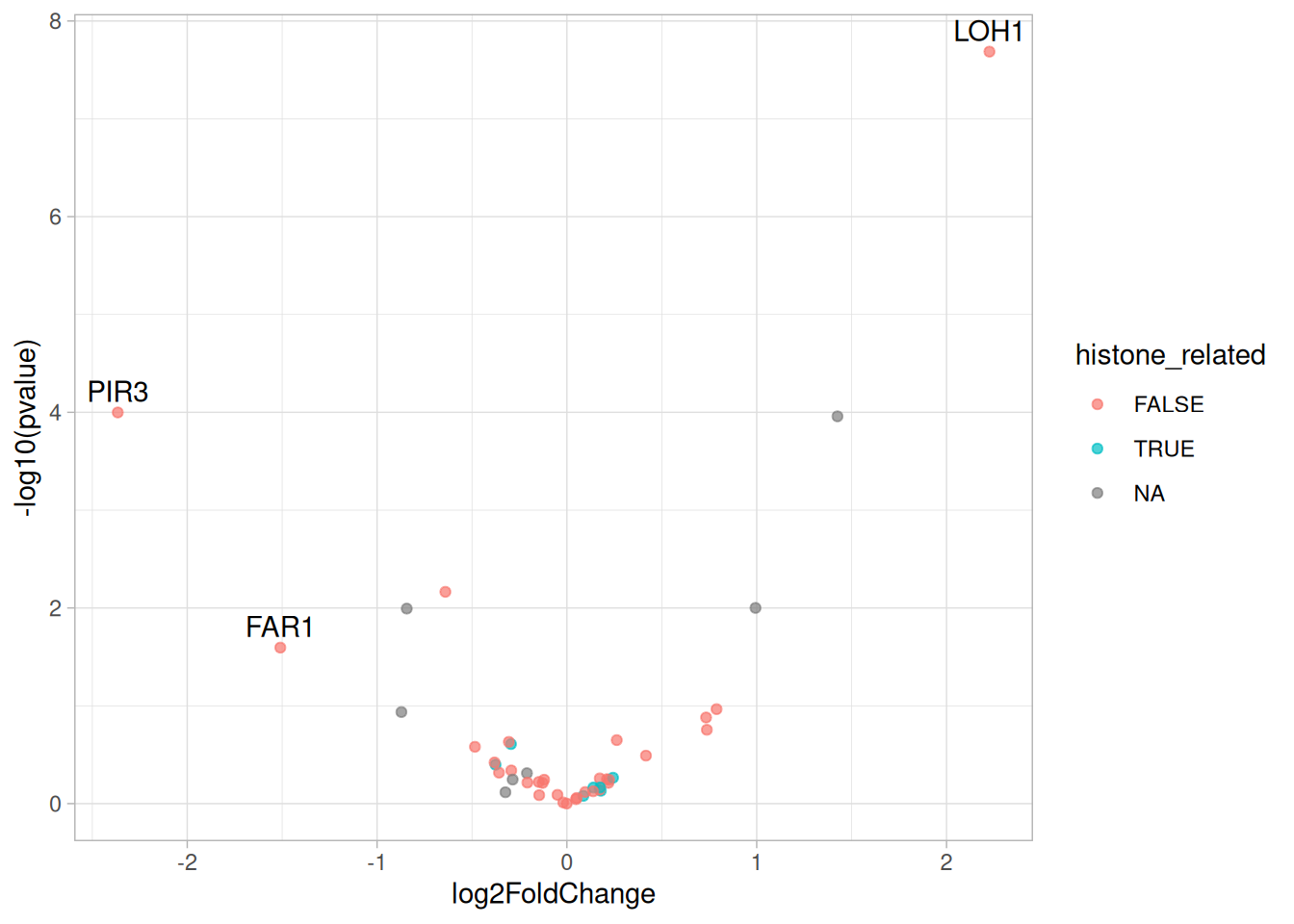
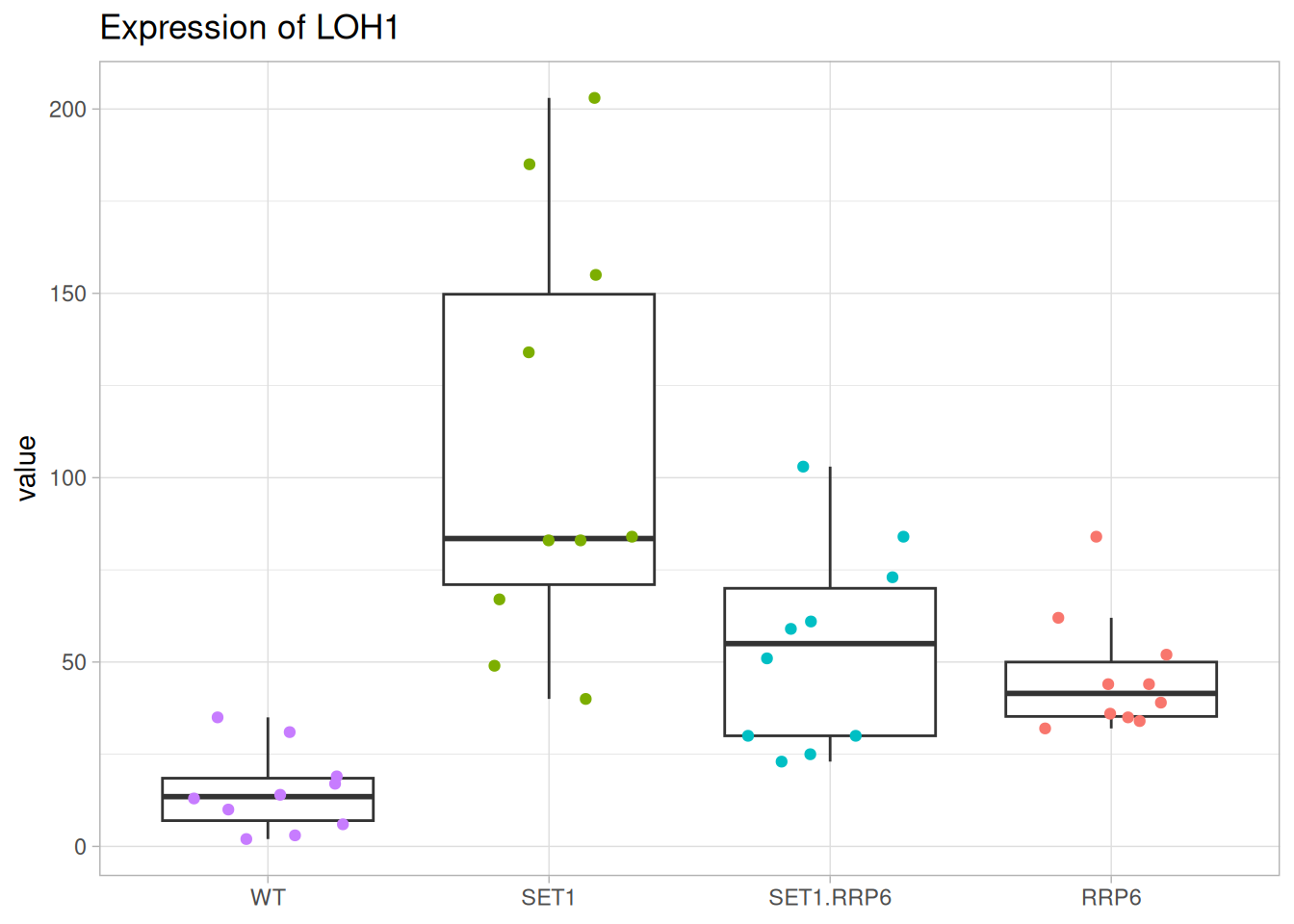
One-way ANOVA
ANOVA (ANalysis Of VAriance) helps us determine whether the means of multiple groups are different. Instead of comparing means directly (as in t-tests), ANOVA compares the variances within (intra) and between groups (inter) to infer differences in means.
We assume that the variance within each group is the same across all groups.
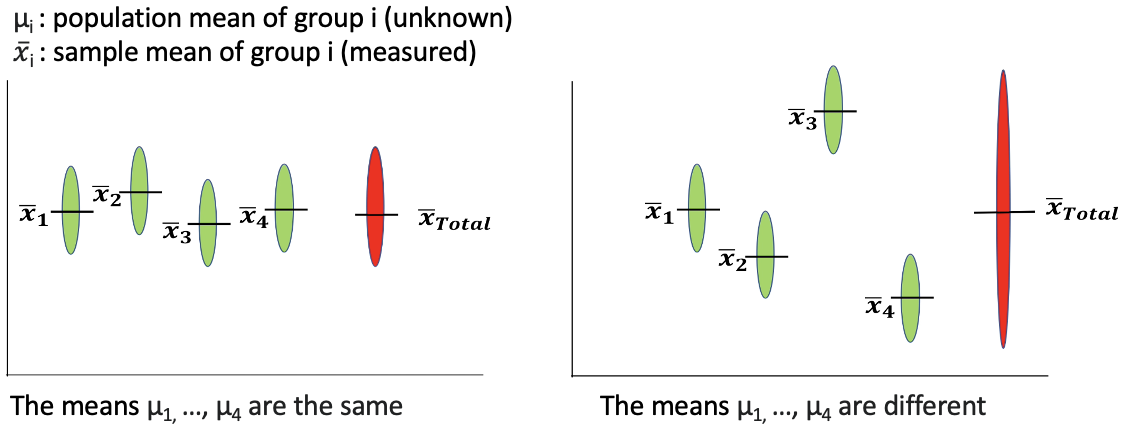
(Figure credit: Lorette Noiret)
- \(H_0: \mu_1 = \mu_2 = ... = \mu_n\)
- \(H_1\): there is at least one group which has an average different than other groups.
Which is equals to test:
- \(H_0: \sigma^2_{\text{inter group}} = \sigma^2_{\text{intra group}}\)
- \(H_1: \sigma^2_{\text{inter group}} > \sigma^2_{\text{intra group}}\)
If the means are truly different, the variation between groups (\(\sigma^2_{\text{inter group}}\)) should be greater than the variation within groups (\(\sigma^2_{\text{intra group}}\)).
ANOVA calculates the F statistic, which is a ratio:
\(F = \frac{\sigma^2_{\text{inter group}}}{\sigma^2_{\text{intra group}}}\)
, and the probability of obtaining an F-statistic as extreme as the observed one (the p-value), assuming the null hypothesis is true.
Conditions of applying ANOVA:
- Independence: Observations in each group must be independent.
- Normality: Data should be approximately normally distributed (can be checked using the Shapiro test).
- Homoscedasticity (homogeneity of variance): Variances across groups should be roughly equal (Levene’s test or Bartlett’s test can check this).
In R, the function aov() is used to perform ANOVA.