Week 3 - Hands-On Examples

week03
exercise

The R script is available here: link

Goals

  • Work with data frames and lists
  • Calculate fold change of gene expression between groups
  • Compare gene expression using the Wilcoxon test
  • Visualize differences with boxplots

Data Frames

Use the following code to import the file “read-counts.csv” (you have already downloaded it for the hand-on examples of week01). Name the imported data expr_data.

expr_data <- read.table(
  file = "../exos_data/read-counts.csv",  # replace the path with your own
  header = TRUE, sep = ",", row.names = 1
)
  1. Check the structure of expr_data using an appropriate R function.
str(expr_data)
'data.frame':   45 obs. of  40 variables:
 $ WT.1        : num  20648 7867 1481 743 185 ...
 $ WT.2        : num  466 147 37 27 6 16 0 105 8 490 ...
 $ WT.3        : num  1783 427 187 370 200 ...
 $ WT.4        : num  25335 5178 1856 4050 669 ...
 $ WT.5        : num  64252 27889 3952 877 166 ...
 $ WT.6        : num  24126 8547 1020 357 68 ...
 $ WT.7        : num  9067 3432 484 845 360 ...
 $ WT.8        : num  19721 6935 1409 2110 595 ...
 $ WT.9        : num  67353 34229 4636 1872 438 ...
 $ WT.10       : num  28059 13913 1870 684 204 ...
 $ SET1.1      : num  21214 9807 1604 1075 209 ...
 $ SET1.2      : num  3822 1663 572 1170 381 ...
 $ SET1.3      : num  2870 932 358 1692 588 ...
 $ SET1.4      : num  65483 31023 7322 10529 1067 ...
 $ SET1.5      : num  39073 30668 3479 753 125 ...
 $ SET1.6      : num  17421 9701 1241 344 93 ...
 $ SET1.7      : num  5979 2484 518 1424 490 ...
 $ SET1.8      : num  29570 12998 3122 5552 1251 ...
 $ SET1.9      : num  56156 39462 5084 1600 346 ...
 $ SET1.10     : num  42195 26192 3027 1120 286 ...
 $ SET1.RRP6.1 : num  36236 34296 4480 3040 1155 ...
 $ SET1.RRP6.2 : num  1716 1238 677 1190 494 ...
 $ SET1.RRP6.3 : num  2137 1672 774 2940 1335 ...
 $ SET1.RRP6.4 : num  21731 18206 4335 9383 2193 ...
 $ SET1.RRP6.5 : num  43086 53296 6548 4044 906 ...
 $ SET1.RRP6.6 : num  33990 35468 3723 1710 402 ...
 $ SET1.RRP6.7 : num  12290 12523 1475 593 183 ...
 $ SET1.RRP6.8 : num  7170 7099 1101 1093 468 ...
 $ SET1.RRP6.9 : num  21650 19932 3824 5620 1940 ...
 $ SET1.RRP6.10: num  21870 23810 3677 2878 893 ...
 $ RRP6.1      : num  38560 32163 3988 2671 959 ...
 $ RRP6.2      : num  4275 1811 941 872 593 ...
 $ RRP6.3      : num  2923 1257 541 2966 1210 ...
 $ RRP6.4      : num  29292 24615 5292 7584 1664 ...
 $ RRP6.5      : num  55453 57599 6436 2714 594 ...
 $ RRP6.6      : num  37863 29579 2844 854 275 ...
 $ RRP6.7      : num  25900 17696 1931 995 517 ...
 $ RRP6.8      : num  21179 14404 2383 5318 1796 ...
 $ RRP6.9      : num  43327 40664 6029 4940 1386 ...
 $ RRP6.10     : num  77043 79181 9389 4092 1267 ...
  1. How many unique values are in sample WT.2?
  • Use unique() to get the unique values;
  • then use length() to check the number of elements.
val_unique <- unique(expr_data[["WT.2"]])
head(val_unique)
[1] 466 147  37  27   6  16
n_unique <- length(val_unique)
n_unique
[1] 33
# all in one line
length(unique(expr_data[["WT.2"]]))
[1] 33
  1. Extract expression levels for the gene “LOH1” in WT samples (WT.1, WT.2, …, WT.10) and SET1 samples (SET1.1, SET1.2, …, SET1.10). Store them as expr_wt and expr_set1. Ensure they are vectors using unlist(). (see help with ?unlist)
expr_wt <- expr_data["LOH1", paste0("WT.", 1:10)]
expr_set1 <- expr_data["LOH1", paste0("SET1.", 1:10)]

# check data structure
str(expr_wt)
'data.frame':   1 obs. of  10 variables:
 $ WT.1 : num 10
 $ WT.2 : num 2
 $ WT.3 : num 14
 $ WT.4 : num 19
 $ WT.5 : num 35
 $ WT.6 : num 17
 $ WT.7 : num 6
 $ WT.8 : num 3
 $ WT.9 : num 31
 $ WT.10: num 13
str(expr_set1)
'data.frame':   1 obs. of  10 variables:
 $ SET1.1 : num 67
 $ SET1.2 : num 49
 $ SET1.3 : num 83
 $ SET1.4 : num 185
 $ SET1.5 : num 203
 $ SET1.6 : num 83
 $ SET1.7 : num 40
 $ SET1.8 : num 84
 $ SET1.9 : num 134
 $ SET1.10: num 155
# convert to vectors
expr_wt <- unlist(expr_wt)
expr_set1 <- unlist(expr_set1)

# check again the structure
str(expr_wt)
 Named num [1:10] 10 2 14 19 35 17 6 3 31 13
 - attr(*, "names")= chr [1:10] "WT.1" "WT.2" "WT.3" "WT.4" ...
str(expr_set1)
 Named num [1:10] 67 49 83 185 203 83 40 84 134 155
 - attr(*, "names")= chr [1:10] "SET1.1" "SET1.2" "SET1.3" "SET1.4" ...
Stats Time!

Fold change

Fold change (FC) measures the relative change in gene expression between two conditions or groups. (e.g., treated vs. untreated, healthy vs. diseased). \[ FC = \frac{Mean Expression in Group 2}{Mean Expression in Group 1} \]

It’s common to log2 transform the fold change :

\[ \begin{aligned} \text{FC} &= 1, \quad \log_2(\text{FC}) = 0 \Rightarrow \text{No change}\\ \text{FC} &= 2, \quad \log_2(\text{FC}) = 1 \Rightarrow \text{Up-regulated} \\ \text{FC} &= 0.5, \quad \log_2(\text{FC}) = -1 \Rightarrow \text{Down-regulated} \end{aligned} \]

  1. Calculate the fold change and log2 fold change for “LOH1” between WT and SET1 groups. Is the gene up- or down-regulated?
## Calculate the mean for each group
avg_wt <- mean(expr_wt)
avg_set1 <- mean(expr_set1)

## Get the fold change
fc <- avg_set1 / avg_wt

## log2 transformed fold change
lfc <- log2(fc)
lfc
[1] 2.851999
Stats Time!

Mann-Whitney Wilcoxon Rank Sum Test

The Wilcoxon Rank Sum test, also called Mann-Whitney test, is a non-parametric test used to compare independant samples (groups). It does not assume a normal distribution.

This test is particularly useful for ordinal data or when the assumptions of parametric tests (like the t-test) are not met.

The idea is to bring the two groups together and sort all values in order.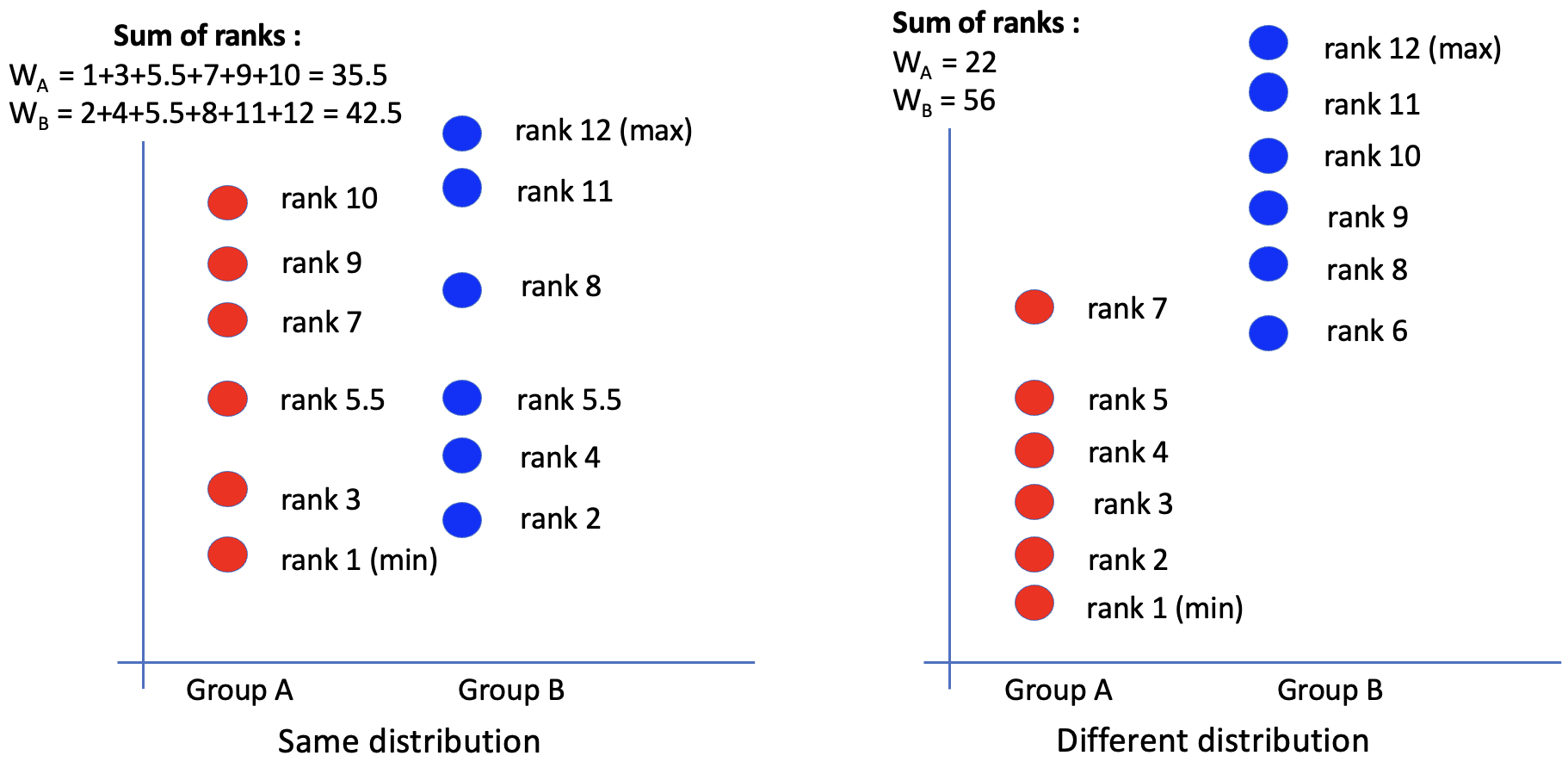

(Figure credit: Lorette Noiret)

The hypotheses are:

  • H0: two groups have the same distribution
  • H1: two groups have different distribution

If H0 is true, then the ranks should be randomly distributed between the two samples (WA ≃ WB). If H0 is false, then the larger ranks will be in one of the two groups (WA < WB)

So we can make decision based on the sum of ranks in each group.

  1. Use wilcox.test() to compare LOH1 expression between WT and SET1. At \(\alpha = 0.05\), what is your conclusion?
wilcox.test(expr_wt, expr_set1)
Warning in wilcox.test.default(expr_wt, expr_set1): cannot compute exact
p-value with ties

    Wilcoxon rank sum test with continuity correction

data:  expr_wt and expr_set1
W = 0, p-value = 0.0001817
alternative hypothesis: true location shift is not equal to 0

As the p-value is smaller than 0.05, we can reject the H0. There is a significant difference between two WT and SET1 samples for the expression of the LOH1.

  1. Create a new data frame for LOH1 gene expression in WT and SET1 samples with two columns:
  • “expr_value”: expression levels
  • “group”: WT or SET1
expr_loh1 <- data.frame(
  expr_value = c(expr_wt, expr_set1),
  group = rep(c("WT", "SET1"), each = length(expr_wt))
)
expr_loh1
        expr_value group
WT.1            10    WT
WT.2             2    WT
WT.3            14    WT
WT.4            19    WT
WT.5            35    WT
WT.6            17    WT
WT.7             6    WT
WT.8             3    WT
WT.9            31    WT
WT.10           13    WT
SET1.1          67  SET1
SET1.2          49  SET1
SET1.3          83  SET1
SET1.4         185  SET1
SET1.5         203  SET1
SET1.6          83  SET1
SET1.7          40  SET1
SET1.8          84  SET1
SET1.9         134  SET1
SET1.10        155  SET1
  1. With the new data frame, draw a boxplot to compare expression between groups using boxplot(). (see ?boxplot)
boxplot(expr_value ~ group, data = expr_loh1)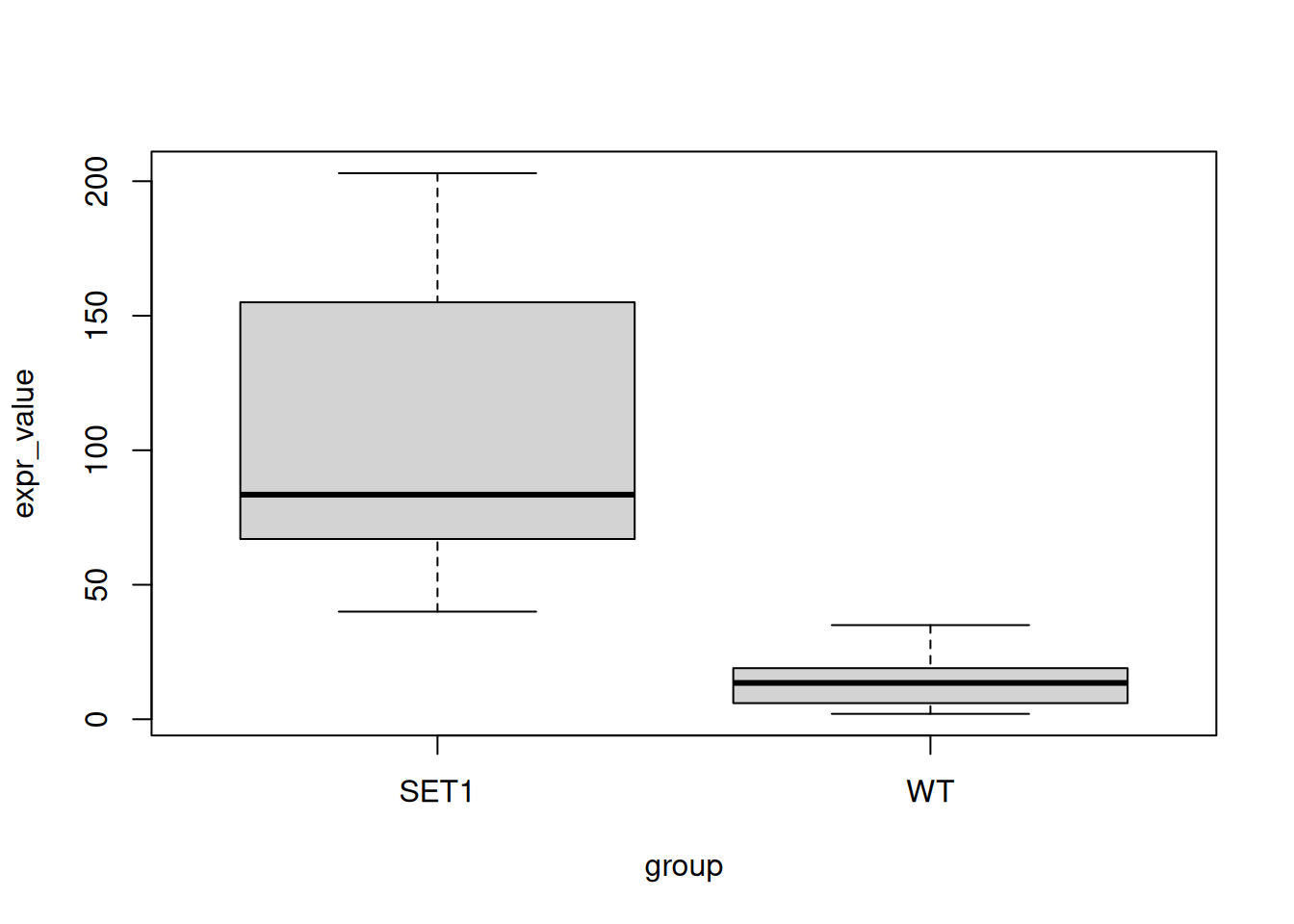

Lists

Here’s a toy list storing information about three samples:

my_list <- list(
  # sample information
  sample_info = data.frame(
    id = paste0("sample", 1:3),
    age = c(25, 27, 30),
    sex = c("F", "M", "F")
  ),
  ## expression matrix
  count_expr = matrix(
    1:6, ncol = 2, dimnames = list(
      paste0("sample", 1:3),
      paste0("gene", c("A", "B"))
    )
  ),
  # mesured genes
  gene_name = paste0("gene", c("A", "B")),
  # sequenced family members of each sample
  family_sequenced = list(
    sample1 = c("father", "mother"),
    sample2 = c("father", "mother", "sister"),
    sample3 = c("mother", "sister")
  )
)
my_list
$sample_info
       id age sex
1 sample1  25   F
2 sample2  27   M
3 sample3  30   F

$count_expr
        geneA geneB
sample1     1     4
sample2     2     5
sample3     3     6

$gene_name
[1] "geneA" "geneB"

$family_sequenced
$family_sequenced$sample1
[1] "father" "mother"

$family_sequenced$sample2
[1] "father" "mother" "sister"

$family_sequenced$sample3
[1] "mother" "sister"
  1. Use names() to extract the names of the elements in the list.
names(my_list)
[1] "sample_info"      "count_expr"       "gene_name"        "family_sequenced"
  1. Extract the count_expr matrix from the list.
my_list[["count_expr"]]
        geneA geneB
sample1     1     4
sample2     2     5
sample3     3     6
  1. From the matrix, find the expression value of geneA in sample2
my_list[["count_expr"]]["sample2", "geneA"]
[1] 2
  1. Calculate the total counts of each gene across all samples.
colSums(my_list[["count_expr"]])
geneA geneB 
    6    15
  1. From sample_info data frame, extract the age column.
my_list[["sample_info"]][["age"]]
[1] 25 27 30
  1. Extract the 1st sequenced family member of sample3.
my_list[["family_sequenced"]][["sample3"]][1]
[1] "mother"
  1. Add a new element to the list, “gene_description”, with the following values: c("geneA" = "housekeeping gene", "geneB" = "stress response gene")
my_list[["gene_description"]] <- c(
  "geneA" = "housekeeping gene",
  "geneB" = "stress response gene"
)
Bonus!

Check out this cheat sheet for the basic R commands: Base R Cheat Sheet

Good job! 👏👏 You’ve taken your first big steps into R, and you’re off to a great start, keep it up!