Week 2 - Hands-On Examples

week02
exercise

The R script is available here: link

Goals

  • Get familiar with variables and data types
  • Get familiar with vectors and matrices manipulations
  • Simulate your own biological data and test the normality using the Shapiro-Wilk test

Variables in R

  • A variable in R is like a labeled container where you can store data (a single value, multiple values, or more complex structures like data frames).
  • Use <- for assignment.

Data Types in R

Create variables to store the following types of biological data and check their class in R:

  1. The name of a gene (e.g., BRCA1).
  2. The number of samples in an experiment (e.g., 50).
  3. Whether a sample is treated or not (select between TRUE/FALSE).
  4. The four bases in DNA sequence: “A”, “T”, “G”, “C”.
gene_name <- "BRCA1" 
is.character(gene_name)
[1] TRUE
num_samples <- 50    
is.numeric(num_samples)
[1] TRUE
is_treated <- TRUE  
is.logical(is_treated)
[1] TRUE
dna_bases <- c("A", "T", "G", "C") 
is.character(dna_bases)
[1] TRUE

Vectors

You have the following concentrations of a drug measured in five samples (in µM): 2.3, 5.1, 3.8, 6.4, 4.9. Perform the following tasks:

  1. Create a numeric vector to store the concentrations.
drug_concentration <- c(2.3, 5.1, 3.8, 6.4, 4.9)
  1. Calculate the mean and standard deviation of the concentrations.
mean_concentration <- mean(drug_concentration)
mean_concentration
[1] 4.5
sd_concentration <- sd(drug_concentration)
sd_concentration
[1] 1.537856
  1. Subset the concentrations greater than 4 µM
high_concentration <- drug_concentration[drug_concentration > 4]
high_concentration
[1] 5.1 6.4 4.9

Matrices

You’re working with expression levels of three genes (geneA, geneB, geneC) across five samples. The expression levels are as follows:

sample1: 10, 12, 15  
sample2: 20, 18, 22  
sample3: 14, 16, 19  
sample4: 8, 9, 7  
sample5: 25, 30, 28
  1. Create a matrix to represent this data, with genes in rows and samples in columns.
# Create the matrix
expression_levels <- matrix(
  c(10, 12, 15,
    20, 18, 22,
    14, 16, 19,
    8, 9, 7,
    25, 30, 28), 
  nrow = 3
)
expression_levels
     [,1] [,2] [,3] [,4] [,5]
[1,]   10   20   14    8   25
[2,]   12   18   16    9   30
[3,]   15   22   19    7   28
## or create first samples' vector then combine them
sample1 <- c(10, 12, 15)
sample2 <- c(20, 18, 22)
sample3 <- c(14, 16, 19)
sample4 <- c(8, 9, 7)
sample5 <- c(25, 30, 28)
expression_levels2 <- cbind(sample1, sample2, sample3, sample4, sample5)
expression_levels2
     sample1 sample2 sample3 sample4 sample5
[1,]      10      20      14       8      25
[2,]      12      18      16       9      30
[3,]      15      22      19       7      28
  1. Add row and column names to the matrix.
# Add row and column names
rownames(expression_levels) <- c("geneA", "geneB", "geneC")
colnames(expression_levels) <- c("sample1", "sample2", "sample3", "sample4", "sample5")

## or
rownames(expression_levels) <- paste0("gene", LETTERS[1:3])
colnames(expression_levels) <- paste0("sample", 1:5)

expression_levels
      sample1 sample2 sample3 sample4 sample5
geneA      10      20      14       8      25
geneB      12      18      16       9      30
geneC      15      22      19       7      28
  1. Calculate the mean expression for each gene (row-wise).
gene_means <- rowMeans(expression_levels)
gene_means
geneA geneB geneC 
 15.4  17.0  18.2
  1. Subset the data to show only samples where geneC expression is greater than 20.
# Extract geneC
geneC_expression <- expression_levels["geneC", ]

# Subset samples with geneC > 20
high_geneC_samples <- geneC_expression[geneC_expression > 20]
high_geneC_samples
sample2 sample5 
     22      28

Test the Normality on Simulated Data

Height

Use following code to generate the height (in cm) of 100 students:

# simulate data following a normal distribution
set.seed(1)
heights <- round(rnorm(n = 100, mean = 170, sd = 10), 1)
heights
  [1] 163.7 171.8 161.6 186.0 173.3 161.8 174.9 177.4 175.8 166.9 185.1 173.9
 [13] 163.8 147.9 181.2 169.6 169.8 179.4 178.2 175.9 179.2 177.8 170.7 150.1
 [25] 176.2 169.4 168.4 155.3 165.2 174.2 183.6 169.0 173.9 169.5 156.2 165.9
 [37] 166.1 169.4 181.0 177.6 168.4 167.5 177.0 175.6 163.1 162.9 173.6 177.7
 [49] 168.9 178.8 174.0 163.9 173.4 158.7 184.3 189.8 166.3 159.6 175.7 168.6
 [61] 194.0 169.6 176.9 170.3 162.6 171.9 152.0 184.7 171.5 191.7 174.8 162.9
 [73] 176.1 160.7 157.5 172.9 165.6 170.0 170.7 164.1 164.3 168.6 181.8 154.8
 [85] 175.9 173.3 180.6 167.0 173.7 172.7 164.6 182.1 181.6 177.0 185.9 175.6
 [97] 157.2 164.3 157.8 165.3
Stats Time!

Normal Distribution

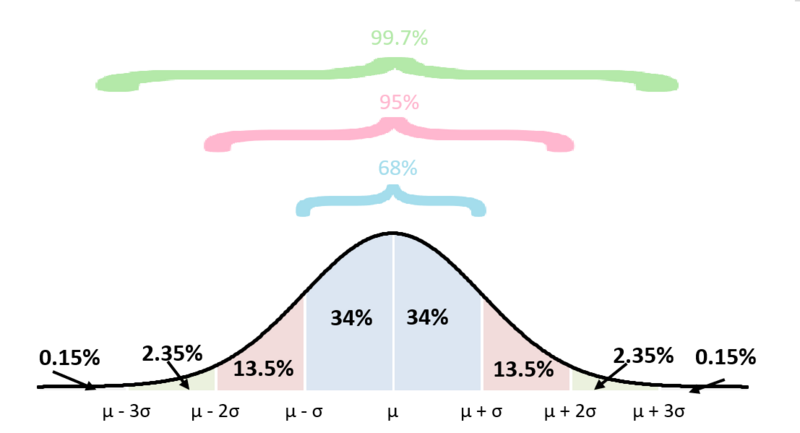
A normal distribution (also known as Gaussian distribution or “bell curve”), is a common way in which data tends to organize itself naturally when measured repeatedly in a population.


(figure obtained from this source)

It’s symmetric around the average (mean, \(\mu\)), and the spread of values depends on the standard deviation (\(\sigma\)). A a smaller \(\sigma\) results in values being tightly concentrated near the mean, while a larger \(\sigma\) results in values being more spread out across the range.

Many statistical tests, such as t-tests or ANOVAs, assume that the data follows a normal distribution. This assumption is important because it enables the calculation of probabilities and supports making reliable inferences. If the data does not follow a normal distribution, these tests may produce misleading results.

Shapiro-Wilk Test

The Shapiro-Wilk test is designed to check for deviations from normality, i.e., to check whether your data follows a normal distribution.

Test Hypotheses: H0, H1

When performing a statistical test, you start with two opposing ideas, called hypotheses, that you want to evaluate:

  • Null Hypothesis (H0): This is the default assumption, often stating that there is no effect, no difference, or no relationship in your data.
  • Alternative Hypothesis (H1): This is the claim you are testing for something different from the null hypothesis.

When you perform a statistical test, the goal is to decide whether you have enough evidence to reject the null hypothesis (H0) in favor of the alternative hypothesis (H1).

The function shapiro.test() in R allows to perform the test of normality.

Here, the null hypothesis (H0) is the heights are normally distributed, and the alternative hypothesis (H1) is the heights are not normally distributed.

shapiro.test(heights) 

    Shapiro-Wilk normality test

data:  heights
W = 0.99564, p-value = 0.9883
Stats Time!

Type I error (\(\alpha\))

A type I error occurs when we reject the null hypothesis whereas it is actually true (false positive).

The probability (risk) of making a type I error is denoted as \(\alpha\), which also called the significance level. By choosing \(\alpha = 0.05\), you’re saying: “I’m willing to accept a 5% chance of incorrectly rejecting H0.”

P-value

The p-value is the probability of observing your data (or something more extreme) if the null hypothesis (H0) is true.

  • If the p-value is small (e.g., ≤ 0.05):
    • There’s strong evidence against H0, so you reject it.
    • This suggests that the alternative hypothesis (H1) might be true.
  • If the p-value is large (e.g., > 0.05):
    • There’s not enough evidence to reject H0.
    • This doesn’t mean H0 is true, it just means the data doesn’t strongly contradict it.

If we take \(\alpha=0.05\): since the p-value (0.9876) is greater than 0.05, we fail to reject H0. This means there’s no strong evidence to suggest the heights are not normally distributed.

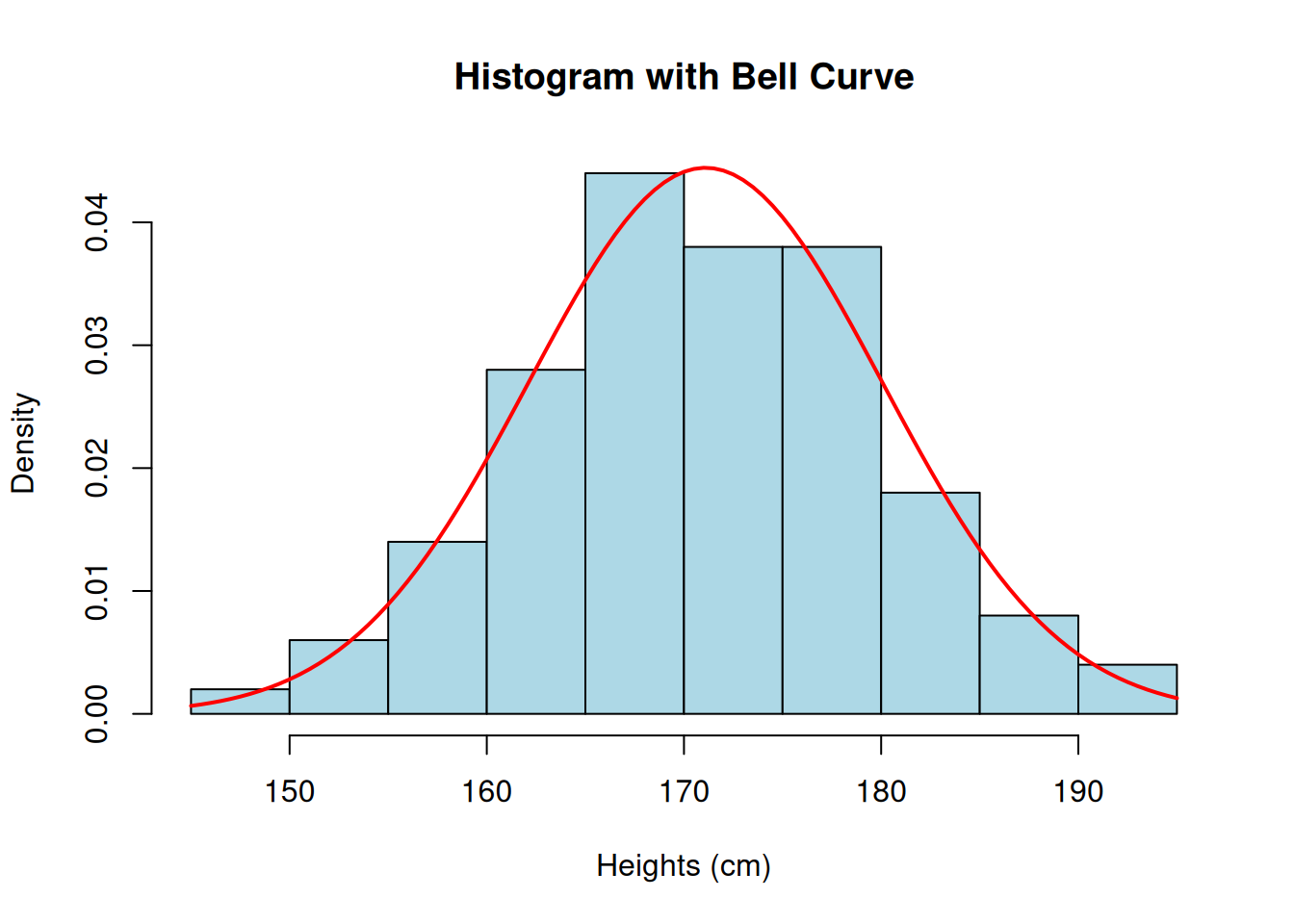
Let’s check the heights’ distribution with a histgram!

# Histogram
hist(
  heights, probability = TRUE, col = "lightblue",
  main = "Histogram with Bell Curve", xlab = "Heights (cm)", ylab = "Density"
)
# Add bell curve
curve(dnorm(x, mean = mean(heights), sd = sd(heights)), col = "red", lwd = 2, add = TRUE)

Good job! 👏👏 You’ve taken your first big steps into R, and you’re off to a great start, keep it up!